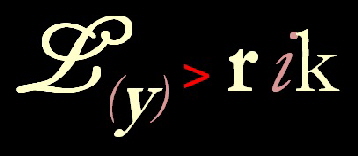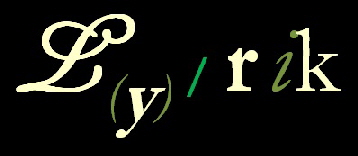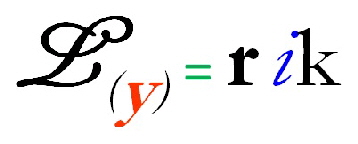Das Parallelenaxiom der poetischen Formel

Auch im Lyrik-Labor rief die poetische Formel sogleich Widerspruch hervor. Denn augenscheinlich konnte für verschiedene Fälle nachgewiesen werden, dass L(y) sowohl größer als auch kleiner r ik sein kann. Gleichheit stellt lediglich einen Spezialfall; eventuell ein ideales oder auch nur idealisiertes Verhältnis dar. Als allgegenwärtiges Maß eignet sich die Labor-Formel selbst für unsere eigenen Gedichte nicht immer.

Doch so rasant, wie die poetische Formel daher kommt, machte sie uns auch neugierig. Denn neben der klassisch euklidischen gibt es seit mehr als hundert Jahren ja auch die elliptische und hyperbolische Geometrie. Hinzu kommt seit etlichen Jahren die fraktale Geometrie, die in unseren Augen eher durch Kontinuität charakterisiert wird. Denn sie setzt Dimensionen in echte Verhältnisse zueinander und kennt auch so etwas wie Skaleninvarianz und Selbstähnlichkeit.

Poetische Formel für hyperbolische Gedichte, Stenkamp #	Poetische Formel für elliptische Gedichte, Stenkamp ##
Poetische Formel für fraktale Gedichte, Stenkamp ###	Poetische Formel für Liebes-Gedichte, Stenkamp ####

Die Verhältnisse werden komplex

 

Startseite  Anwendungen  Gedichte A-Z  AutorInnen  Das Labor  Quellen  Studieren  Sitemap  Impressum  Datenschutz  Kontakt